왜 Conformal Prediction이 필요한가?

머신러닝 모델의 블랙박스 특성과 예측 불확실성 문제를 해결하기 위한 Conformal Prediction(정합 예측) 방법론을 소개합니다. 단일 예측값이 아닌, 통계적으로 보장된 신뢰수준을 갖는 '예측 집합'을 통해 모델의 확신도를 직관적으로 파악하는 원리와 그 장점을 알아봅니다. AI의 신뢰도를 한 단계 높이는 방법에 대해 확인해 보세요.

Photo by Gayatri Malhotra / Unsplash

✍️

Conformal Prediction 세미나를 준비하면서 남겨보고 싶은 내용들을 블로그 글로 정리합니다. 이 태그를 통해 세미나 관련 글을 읽을 수 있습니다.

💡

선결론. Conformal Prediction은 모델의 불확실성을 표현한다.

학부생 시절, 제가 ML등의 여러 AI 이론들을 공부하면서 항상 어색하게 느낀 부분이 있다. 바로 블랙박스 (Black box) 라는 특성이다. 기존 통계적 모델의 경우 어느정도 이론적 증명이 가능하지만, 최신 연구에서 쓰이는 대형 모델들은 내부 구조가 구체적으로 추정되지 않는 경우도 있다. 블랙박스 때문에 내부 구조를 최대한 설명하려고 하는 설명가능한 AI (Explainable AI) 분야도 꾸준히 연구중이다.

이러한 문제를 마주하면 모델에 대한 신뢰도에 대한 의문도 생길 것이다. 보통 대다수의 모델들은 입력된 데이터에 대해 가장 확률이 높다고 판단되는 단 하나의 예측값을 출력한다. 예를 들어 이미지 대상을 예측하는 모델이 90%, 95%의 확신을 가지고 고양이임을 예측하면 충분히 신뢰가 있을 것이다. 그런데 한 20%의 확신을 가지고 고양이임을 예측했는데 그 확신이 가장 커서 결과값으로 고양이를 출력한다면? 그 결과값을 신뢰할 수 있을까?

이미지 대상을 예측하는 모델을 만들었을 때, 다음과 같은 확률로 서점이 아닌 감옥으로 나올 것이다.

이러한 상황은 기존 모델들이 예측의 불확실성(Uncertainty) 을 제대로 표현하지 못하는 것에서 비롯된다. 모델이 얼마나 확신을 가지고 예측을 하는지, 예측이 틀릴 가능성이 어느 정도인지에 대한 정보를 제공하지 않는 한계가 있다. 특히 의료, 금융, 자율주행 등 높은 신뢰성이 요구되는 분야에서는 이러한 불확실성 정보의 부재가 치명적인 약점을 보여줄 수 있다.

Conformal Prediction은 모델의 불확실성을 표현한다

Conformal Prediction(정합 예측, 이하 CP)은 이러한 기존 모델의 한계를 극복하기 위해 등장한 통계적 방법론이다. 이 방법론은 통계학의 신뢰 구간(Confidence Interval)의 개념과 유사하게 생각하면 쉽다. CP는 위처럼 단 하나의 예측값을 제시하는 것이 아니라 실제 정답이 특정 신뢰수준 하에 (예를 들어 95%의 확률로) 포함될 것으로 보장되는 예측값의 집합을 제공하는 것이 핵심이다.

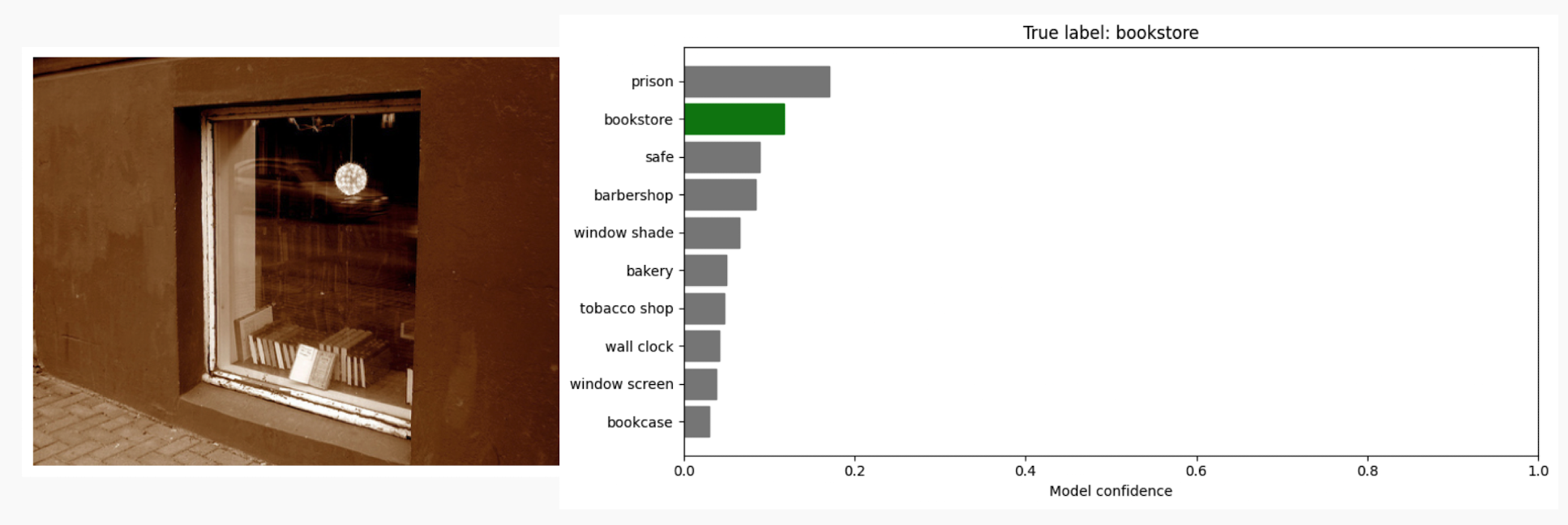
위 예시를 들고오자면 주어진 사진에 대해 "prison"이라고 단일 결과를 주는게 아니라 {"prison", "bookstore", "safe", "barbershop"} 와 같이 여러 결과의 집합으로 출력하는 것이다. 이렇게 결과를 단일결과가 아니라 집합, 구간으로 주어지게 된다면 이 결과물을 가지고 모델의 불확실성을 파악할 수 있을 것이다. 만약 모델이 예측에 자신이 있다면 이 집합의 크기는 작아질 것이고, 자신이 없다면 집합의 크기는 커질 것이다. 해당 부분으로 모델의 불확실성을 직관적으로 파악할 수 있게 된다.

How?

CP는 Conformal score function(적합성 점수)이라는 개념을 사용한다. 해당 함수는 모델의 예측이 얼마나 비순응적(non-conformal)인지 정량화하는 점수이다. 모델이 해당 데이터에 비순응한다면 큰 값을, 순응한다면 작은 값을 주는 함수인 것이다. 대표적인 conformal score function의 예시는 residual score, $s(x, y) = |y-\hat{f}(x)|$이다. 여기서 $y$는 실제 정닶값, $\hat{f}(x)$는 모델의 예측값을 의미하기에, 이 score는 '실제값과 예측값의 차이'를 비적합성 점수로 사용하는 것이다.

CP는 conformal score funtion을 기반으로 주어진 신뢰수준에 해당하는 함수값 임계값을 찾는다. 새로운 데이터에 대한 예측을 수행할 때, 가능한 모든 예측값에 대해 conformal score를 계산하고, 이 점수가 임계값보다 낮은 예측값들만 모아 최종 예측 집합을 구성한다.

가장 단순한 CP Algorithm. Angelopoulos et al, 2024

💡

구체적인 방식에 대해서는 이후 포스팅을 통해 설명할 예정이다.

CP가 가지는 이점

특히 CP는 다음과 같은 장점들이 있다 보니 각광받고 있다.

통계적으로 보장되는 신뢰도

CP를 설계할 때, 직접 원하는 신뢰수준을 설정하고 그 수준에 맞는 예측 결과를 얻을 수 있다. 또한 이는 데이터 분포에 대한 특별한 가정이 필요 없는, 통계적으로 엄격하게 보장되는 결과이다.

최소한의 가정으로 넓은 적용 범위

위에서 언급한대로, CP는 특정 머신러닝 모델에 종속되지 않는다. 특정 분포를 가정하지 않더라도 설계할 수 있다. 이는 비모수통계학 (Nonparametric) 보다 더 약한 가정으로도 가능하다. CP에서는 Exchangeability (교환가능성) 가정만 있다면 설계가 가능하다.

💡

Exchangeability 는 이 글을 통해 확인할 수 있다.

직관적인 해석

위 예시처럼 예측 집합, 구간의 크기는 모델의 불확실성을 직접적으로 나타낸다. 집합이 크다는 것은 모델이 해당 예측에 대해 확신하지 못한다는 의미이며, 이를 바탕으로 후속 조치를 결정할 수 있다. 예를 들어, 예측 집합이 너무 큰 경우에는 전문가의 추가적인 검토를 요청하는 등의 의사결정이 가능하다.

Blackbox의 '왜'는 몰라도 '얼마나 믿을지'는 알려주는 기술

AI 기술이 발전함에 따라 우리는 AI에게 더 많은 것을 요구하게 될 것이다. 단순히 정확한 예측을 넘어, 그 예측이 얼마나 신뢰할 수 있는지에 대한 정보까지 요구하게 될 것이다. CP은 이러한 요구에 부응하는 유용한 도구이다.

물론 CP이 모든 문제를 해결하는 만능 해결책은 아닙니다. 약하지만 Exchangeability 가정이 필요하며, 예측 집합의 크기가 너무 커져 실용성이 떨어지는 경우도 발생할 수 있다. 하지만 이러한 한계에도 불구하고, CP이 제공하는 '신뢰할 수 있는 불확실성'이라는 가치는 AI 시스템의 안정성과 투명성에 대해 발전시킬 수 있을 것이다.

참고문헌

Angelopoulos, Anastasios N., Rina Foygel Barber, and Stephen Bates. 2024. “Theoretical Foundations of Conformal Prediction.” arXiv [Math.ST]. arXiv. https://arxiv.org/abs/2411.11824.
Angelopoulos, Anastasios N., and Stephen Bates. 2021. “A Gentle Introduction to Conformal Prediction and Distribution-Free Uncertainty Quantification.” arXiv [Cs.LG]. arXiv. https://arxiv.org/abs/2107.07511.