손실 함수와 평가지표 - 회귀 모델

손실 함수와 평가지표 - 회귀 모델
Photo by ThisisEngineering / Unsplash

ML 모델을 사용하다 보면 A모델보다 B모델이 더 좋은데 그걸 비교할 땐 MSE, MAE, WQL 등 다양한 지표를 사용한다. 자주는 사용하지만 워낙 종류가 많아 햇갈리기도 하는데 이 글을 통해 여러 지표들을 정리할까 한다.

손실 함수

손실 함수(Loss Function)는 모델이 예측한 값과 실제 값 사이의 차이, 즉 오차를 측정하는 함수이다. 머신러닝 모델은 학습 과정에서 이 손실 함수가 반환하는 값을 최소화하는 방향으로 파라미터를 업데이트한다. 따라서 어떤 손실 함수를 사용하느냐에 따라 모델의 학습 방식과 성능이 달라질 수 있다. 따라서 이런 평가지표는 모델을 평가하는 관점에서도 볼 수 있지만, 모델을 학습하는 관점에서는 손실 함수로도 볼 수 있다.

회귀 모델에서의 지표

보통 이런 손실 함수는 문제, 데이터의 형태마다 다르게 설정되는데 이번 글에서는 회귀(Regression) 문제에 대한 손실 함수, 평가지표를 정리할 예정이다. 여기에 있는 대부분의 함수들은 통계학의 회귀분석 분야에서 자주 쓰이는 함수이기도 하다.

  • L1 loss, L2 loss
  • MSE, RMSE
  • MAE

Notation

  • (train, test 등 다양한) 데이터 집합 : $ \mathcal{D} = \{(x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)\} $
    • 설명 변수 (Covariate, input) : $x_1, \cdots, x_n$
    • 반응 변수 (response, output) : $y_1, \cdots, y_n$
    • 데이터의 갯수 : $n$
  • 가능한 모델 : $f \in \mathcal{F}$
  • 모델의 예측값 : $\hat{y_i} := f(x_i)$

L1 loss, L2 loss

L1 loss, L2 loss는 회귀 문제에서 사용되는 가장 기본적인 손실 함수이다. 이는 L1, L2 norm이라고도 부르는데, 이 부분이 궁금하다면 수학적인 블로그 글을 읽어보면 좋을 것 같다.

L1 loss

$$ l_{L_1}(y_i, \hat{y_i}) := \sum_{i=1}^n |y_i - \hat{y_i}| $$

L2 loss

$$ l_{L_2}(y_i, \hat{y_i}) := \sum_{i=1}^n (y_i - \hat{y_i}) ^2 $$

L1과 L2 loss는 실제 값과, 예측 값의 차이에 절댓값을 취하냐, 아님 제곱을 취하냐의 차이인데, 이 차이는 이상치(outlier)에 대해 서로 다르게 반응한다. 아래 그래프를 참고하면, 확실히 제곱을 취하면 이상치에 민감하고, 절대값은 제곱에 비해 이상치에 둔감하다. 해당 부분은 이후 데이터의 특징에 맞게 선택하는 것이 필요하다.

y축 scale이 훨신 큼에 유의해 확인해보자.

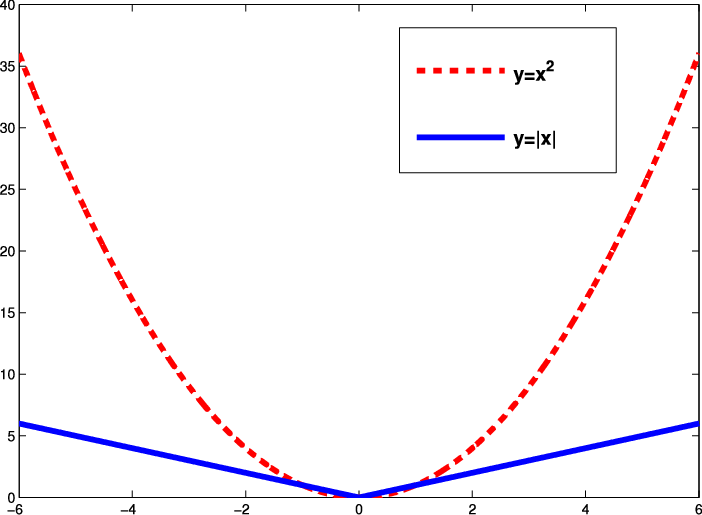
이러한 손실 함수들은 모델의 가중치를 규제(Regularization)하여 과적합(Overfitting)을 방지하는 데에도 활용된다. L1 Lasso는 L1 loss을, L2 Ridge는 L2 loss을 사용하여 특정 가중치를 0에 가깝게 만들거나 전체적으로 가중치의 크기를 줄이는 역할을 한다.

MSE, RMSE

MSE (Mean Squared Error, 평균 제곱 오차) 는 L2 loss 형태에 평균을 내는 것으로 이해할 수 있다.

$$ MSE := \frac1n\sum_{i=1}^n (y_i - \hat{y_i}) ^2 $$

그렇다면 L2 loss를 쓰면 되지 왜 MSE를 사용하는가? 보통은 L2 loss는 모델 학습시 사용하는 손실함수의 입장에서 많이 쓰이고, MSE는 모델 성능 평가 지표로써 많이 쓰인다. 특히 모델 간 비교를 할 때 각 모델의 데이터 수가 다른 경우에는 L2 loss 형태로 본다면 갯수에 대한 scaling이 들어갈 수 밖에 없다. 따라서 이를 비교하기 위해 평균을 낸다고 볼 수 있다.

당연히 형태가 비슷하기에 L2 loss의 특징인 이상치에 민감하다는 특징을 MSE도 가지고 있다. 그래서 이를 보완한 RMSE (Root Mean Squared Error, 평균 제곱근 오차) 도 많이 쓰인다.

$$ RMSE := \sqrt{\frac1n\sum_{i=1}^n (y_i - \hat{y_i}) ^2} = \sqrt{MSE} $$

MAE

반대로 MAE (Mean Absolute Error, 평균 절대 오차) 는 L1 loss 형태에 평균을 내는 것으로 이해할 수 있다.

$$ MAE := \frac1n\sum_{i=1}^n |y_i - \hat{y_i}| $$

그럼 이런 의문이 생길 것이다. RMSE 도 MSE에 루트를 씌웠음으로 L2 loss의 이상치에 민감하지 않게 수정했는데, MAE가 있는데 왜 RMSE도 만들었을까? 일단 MAE의 경우에는 모든 오차에 대해 동일한 가중치를 부여한다. 반면, RMSE의 경우 제곱의 성질상 1보다 작은 오차에 대해서는 더 작게, 1보다 더 큰 오차에 대해서는 더 크게 반영이 된다. 따라서 "이상치에 민감하다" 는 측면에서는 RMSE가 상대적으로 MAE에 비해 민감하다고 할 수 있다.

확실히 RMSE가 outlier를 더 크게 반영된다.

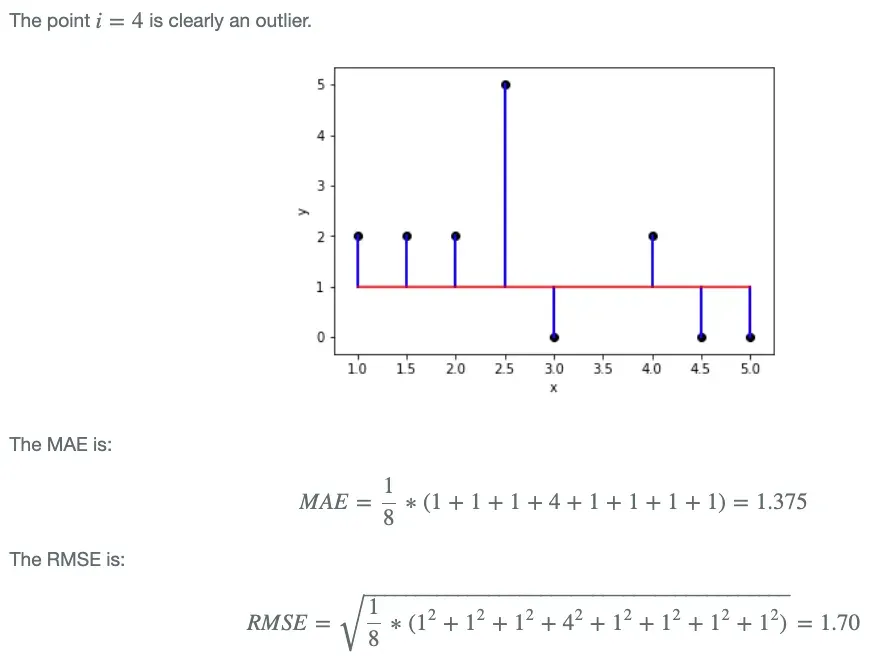
그렇다면 MAE를 쓰면 되지 않을까 싶지만, 이 두 지표를 손실 함수의 입장에서 보고 GD (Gradient Descent, 경사하강법) 에서 사용한다고 하면, MAE는 미분값을 1, -1 혹은 미분값을 가지지 않는 세가지 경우로 나눠지지만, RMSE의 경우 미분값을 가지지 않는 0을 제외하면 연속적인 미분값을 가진다. 이런 측면에서는 확실히 RMSE가 MAE 보다 학습 측면에서는 도움이 된다.

참고문헌