Gaussian Process : 함수에 대한 확률분포
유한 개 점에서는 다변량 정규분포, 관측 후에는 조건부 정규분포. Gaussian Process의 핵심 아이디어를 정리했다.

Bayesian Optimization을 공부하다 보면 반드시 마주치게 되는 개념이 바로 Gaussian Process(GP)다. GP는 "함수 공간 위의 확률분포"라는 다소 추상적인 개념인데, 처음 접하면 직관이 잘 안 잡힌다. 이 글에서는 GP가 무엇인지, 왜 유용한지를 최대한 직관적으로 설명해보려 한다.
계산하기 힘든 함수를 최적화
다음과 같은 최적화 문제를 생각해보자.
$$ x^* = \arg\max_{x \in \mathcal{X}} f(x) $$
여기서 $f$는 평가 비용이 매우 큰 함수다. 예를 들어 하이퍼파라미터 튜닝을 생각해보면, 한 번 $f(x)$를 평가하려면 모델 전체를 학습시켜야 한다. 시간도 돈도 많이 든다. 게다가 관측값에는 노이즈까지 섞여 있을 수 있다.
$$ y = f(x) + \varepsilon, \quad \varepsilon \sim \mathcal{N}(0, \sigma_n^2) $$
이런 상황에서 우리는 제한된 평가 횟수 안에서 최적해를 찾아야 한다. 그렇다면 "다음에 어디를 평가할까?"를 결정하는 전략이 필요하다. 이를 위해 현재까지의 관측 데이터를 바탕으로 $f$가 어떻게 생겼을지 추론해야 한다.
함수를 확률변수로?
Bayesian 접근법의 핵심은 미지의 목적함수 $f$를 확률변수로 취급하는 것이다. 데이터를 보기 전에는 $f$에 대한 사전 믿음(prior)이 있고, 데이터를 관측한 후에는 Bayes rule을 통해 사후 믿음(posterior)으로 업데이트한다.
$$ p(\phi \mid \mathcal{D}) = \frac{p(y \mid x, \phi) , p(\phi \mid x)}{p(y \mid x)} $$
여기서 $\phi = f(x)$다. 문제는 우리가 추론하고 싶은 건 특정 점 $x$에서의 함수값 $\phi$가 아니라 함수 전체 $f: \mathcal{X} \to \mathbb{R}$라는 것이다. 함수 전체에 대한 확률분포를 어떻게 정의할 수 있을까?
이때 등장하는 것이 바로 **확률과정(stochastic process)**이다. 그리고 그 중에서도 수학적으로 다루기 편한 것이 Gaussian Process다.
Gaussian Process의 정의
Gaussian Process는 다음과 같이 정의된다.
Definition. 함수 $f: \mathcal{X} \to \mathbb{R}$가 Gaussian Process를 따른다는 것은, 도메인의 임의의 유한 부분집합 $\mathbf{x} = {x_1, \ldots, x_n} \subset \mathcal{X}$에 대해 $\bm{\phi} = f(\mathbf{x}) = (f(x_1), \ldots, f(x_n))^\top$가 다변량 정규분포를 따른다는 것이다.
GP는 평균 함수 $\mu$와 공분산 함수(커널) $K$로 완전히 특정된다.
$$ p(f) = \mathcal{GP}(f; \mu, K) $$
이때
$$ \mu(x) = \mathbb{E}[\phi \mid x], \quad K(x, x') = \text{cov}[\phi, \phi' \mid x, x'] $$
임의의 유한 집합 $\mathbf{x}$에 대해
$$ p(\bm{\phi} \mid \mathbf{x}) = \mathcal{N}(\bm{\phi}; \bm{\mu}, \bm{\Sigma}) $$
를 만족하고, 여기서 $\bm{\mu} = \mu(\mathbf{x})$이고 $\bm{\Sigma}_{ij} = K(x_i, x_j)$다.
이렇게 유한 차원에서의 분포만 지정해도 되는 이유는 Kolmogorov Extension Theorem 덕분이다. 이 정리는 일관성(consistency) 조건을 만족하는 유한 차원 분포들이 주어지면, 무한 차원의 확률과정이 유일하게 존재한다는 것을 보장한다. 다변량 정규분포는 마진화할 때 부분 공분산 행렬만 취하면 되므로 이 조건을 자연스럽게 만족한다.
예시: Squared Exponential Kernel
가장 흔히 쓰이는 커널은 Squared Exponential(SE) 커널이다.
$$ K(x, x') = \exp\left(-\frac{1}{2}|x - x'|^2\right) $$
이 커널의 특징은 다음과 같다.
- $K(x, x) = 1$: 모든 점에서 분산이 1이다
- 거리가 가까울수록 상관관계가 높다
- 이는 연속성에 대한 통계적 믿음을 보여준다
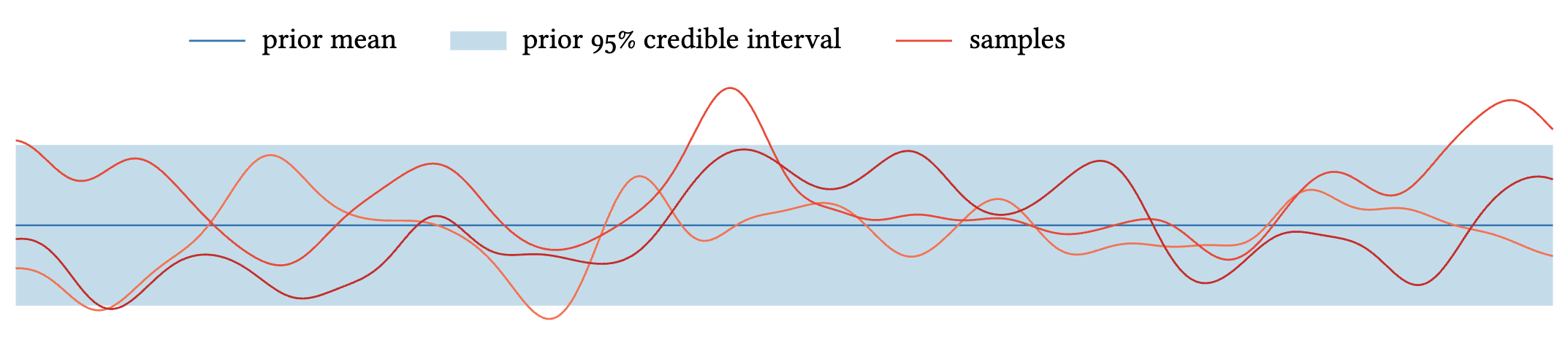
위 그림은 평균 $\mu \equiv 0$, SE 커널을 사용한 GP에서 샘플링한 함수들이다. 함수들이 부드럽게 변하는 것을 볼 수 있는데, 이는 가까운 점들이 높은 상관관계를 가지기 때문이다.
GP에서의 추론: 조건부 분포
GP의 큰 장점중 하나는 관측값이 주어졌을 때의 조건부 분포를 닫힌 형태로 계산할 수 있다는 점이다.
위치 $\mathbf{x}$에서 함수값 $\bm{\phi} = f(\mathbf{x})$를 정확히 관측했다고 하자. 이때 posterior GP는 다음과 같다.
$$ p(f \mid \mathcal{D}) = \mathcal{GP}(f; \mu_{\mathcal{D}}, K_{\mathcal{D}}) $$
$$ \mu_{\mathcal{D}}(x) = \mu(x) + K(x, \mathbf{x}) \bm{\Sigma}^{-1}(\bm{\phi} - \bm{\mu}) $$
$$ K_{\mathcal{D}}(x, x') = K(x, x') - K(x, \mathbf{x}) \bm{\Sigma}^{-1} K(\mathbf{x}, x') $$
여기서 $\bm{\Sigma} = K(\mathbf{x}, \mathbf{x})$다.
직관적으로, 이미 관측한 점에서는 불확실성이 없고, 관측점에서 멀어질수록 불확실성이 커진다.
노이즈가 있는 관측
실제 상황에서는 관측에 노이즈가 섞여 있는 경우가 대부분이다.
$$ \mathbf{y} = \bm{\phi} + \bm{\varepsilon}, \quad \bm{\varepsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{N}) $$
이 경우 posterior 공식에서 $\bm{\Sigma}$를 $\bm{\Sigma} + \mathbf{N}$으로 바꾸기만 하면 된다.
$$ \mu_{\mathcal{D}}(x) = \mu(x) + K(x, \mathbf{x})(\bm{\Sigma} + \mathbf{N})^{-1}(\mathbf{y} - \bm{\mu}) $$

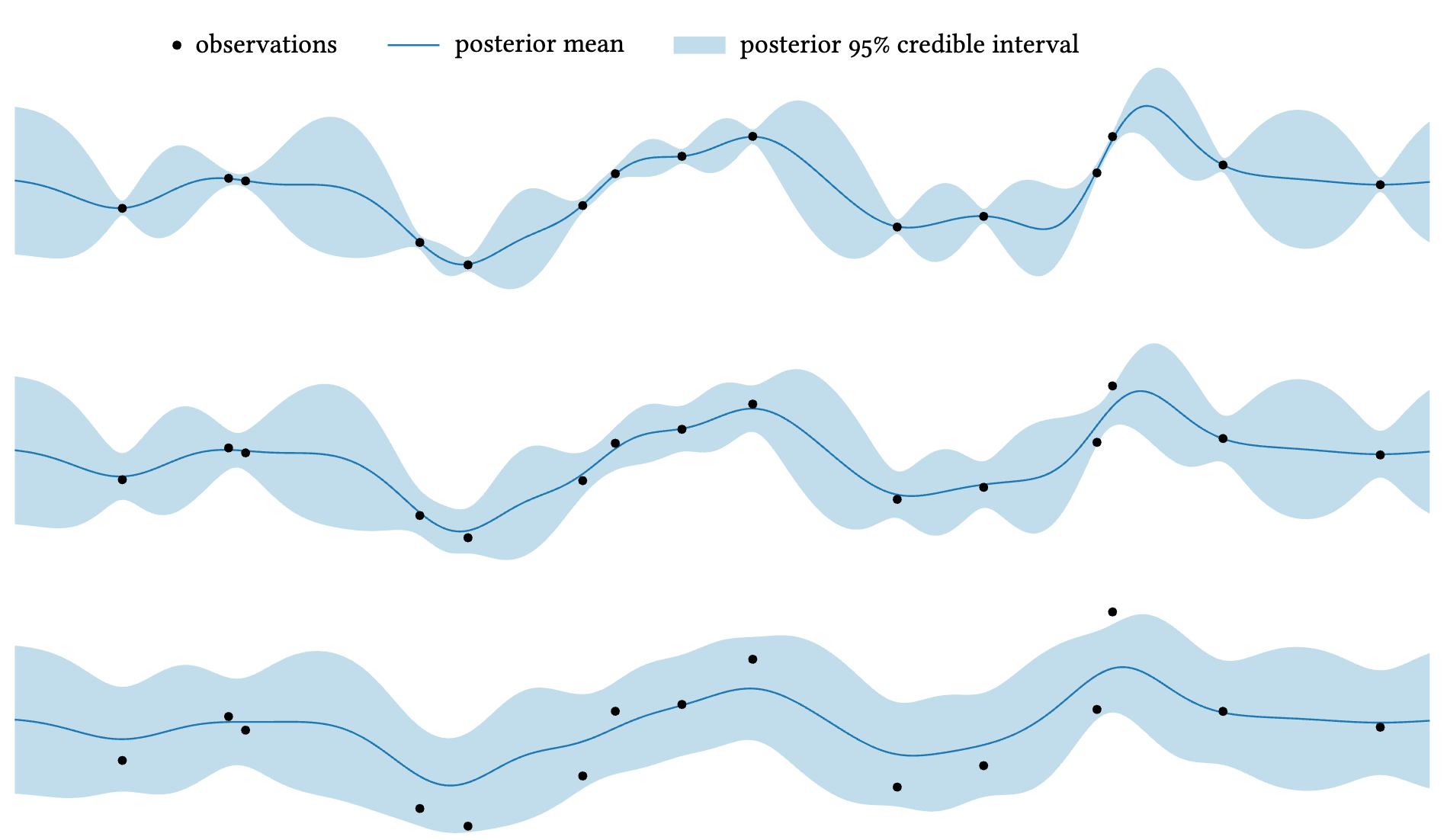
위 그림은 같은 관측 위치에서 노이즈 수준이 증가할 때 posterior가 어떻게 변하는지 보여준다. 노이즈가 클수록 posterior mean이 관측값을 정확히 지나지 않고, 불확실성(shaded region)도 더 커진다.
Posterior Moments의 해석
단일 관측 $y$가 있을 때 posterior를 더 직관적으로 이해할 수 있다. $z$-score와 상관계수를 정의하면
$$ z = \frac{y - m}{s}, \quad \rho = \text{corr}[y, \phi \mid x] = \frac{\kappa(x)}{\sigma s} $$
Posterior moments는 다음과 같이 표현된다.
$$ \text{Posterior mean of } \phi : \mu + \sigma \rho z $$
$$ \text{Posterior std of } \phi : \sigma \sqrt{1 - \rho^2} $$
이 공식은 이렇게 해석할 수 있다.
- 평균의 이동은 $z$-score(관측이 얼마나 예상과 다른가)와 상관계수(관측과 예측 대상이 얼마나 관련 있는가)에 비례한다
- 분산의 감소는 오직 상관계수의 크기에만 의존한다
마무리
GP는 함수 공간 위의 확률분포라는 추상적인 개념이지만, 핵심 아이디어는 단순하다.
- 유한 개의 점에서는 다변량 정규분포
- 관측값이 주어지면 조건부 정규분포로 업데이트
- 커널이 함수의 성질(smoothness, periodicity 등)을 해석
References
- Garnett, R. (2023). Bayesian Optimization. Cambridge University Press.
- Rasmussen, C. E., & Williams, C. K. I. (2006). Gaussian Processes for Machine Learning. MIT Press.