Double Descent : Overfitting이 끝이 아니다

딥러닝 모델의 loss가 overfitting 이후 다시 개선되는 Double Descent 현상을 소개합니다. 전통적인 bias-variance tradeoff를 넘어, 왜 GPT와 BERT 같은 거대 모델들이 성공하는지 Belkin et al. 2019 연구를 통해 설명합니다. Interpolation threshold, over-parameterized regime 등 핵심 개념과 실무 활용법을 다룹니다.

Photo by Ralph Mayhew / Unsplash

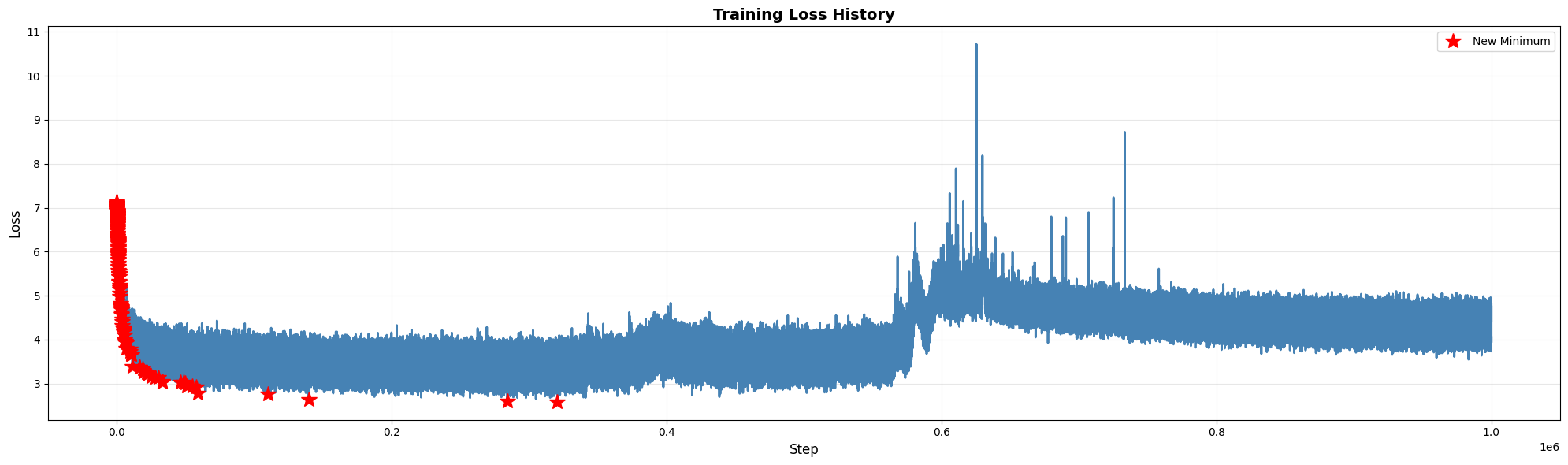
지난번 교수님과의 연구 미팅중 현재 필자가 학습하는 모델에 대해서 loss 그래프를 보다가, 해당 모델이 Double Descent일수도 있다는 조언을 해주셨다. 여태까지는 일반적인 ML 모델은 특정 시점이 지나면 overfitting 한다는건 알고있었지만, Double Descent라는 용어 자체를 처음 들어서 이번 글을 통해 정리해보자 한다.

Bias-Variance Tradeoff

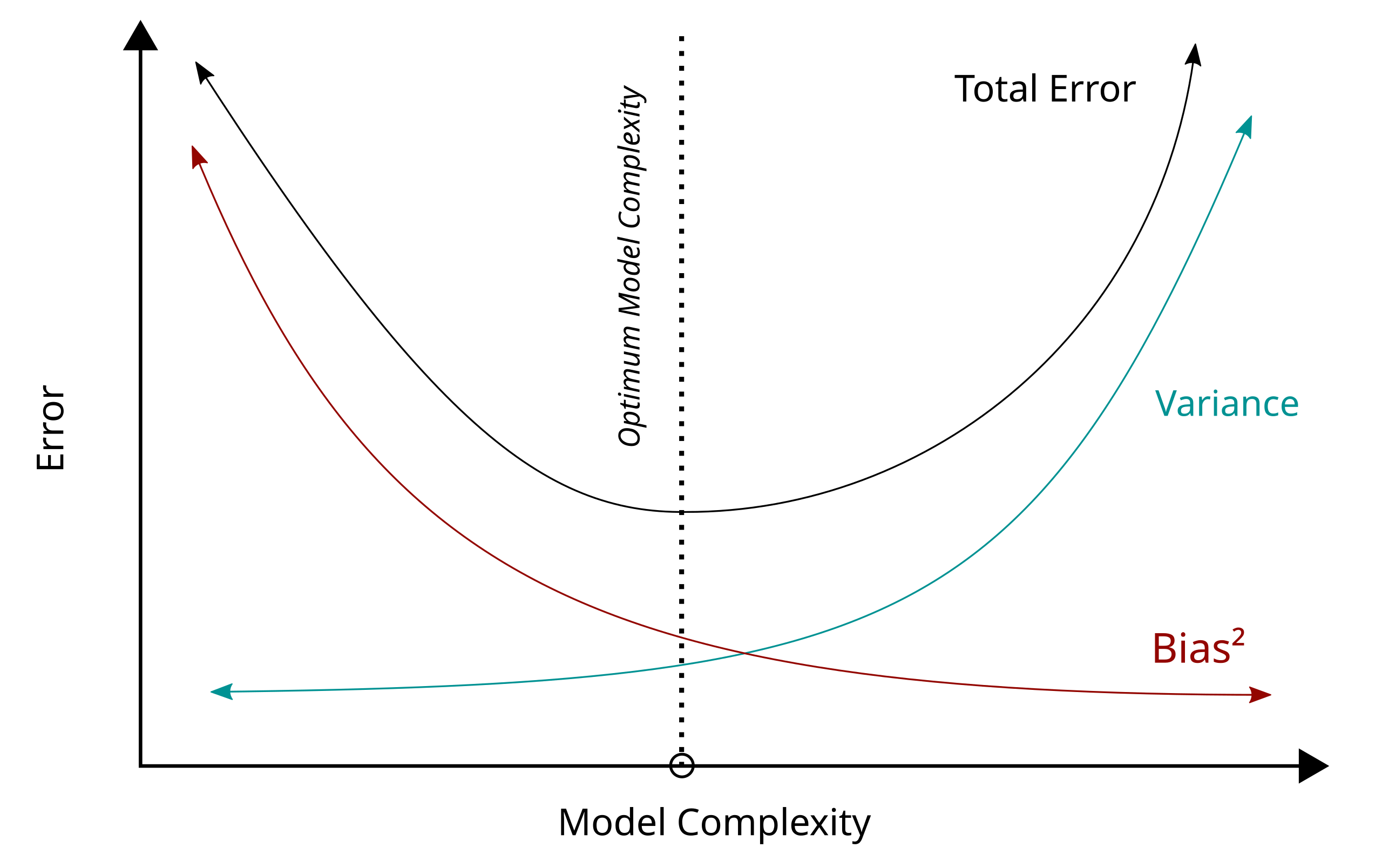
머신러닝을 처음 배울 때, Bias-variance tradeoff라는 개념을 배운다. 모델이 너무 단순하면 underfitting, 너무 복잡하면 overfitting이 일어난다는 고전적인 개념이다. Test error는 U자 형태의 곡선을 그리며, 우리의 목표는 이 곡선의 최저점을 찾는 것이라고 배운다.

대형 모델에서 발생하는 Double Descent 현상

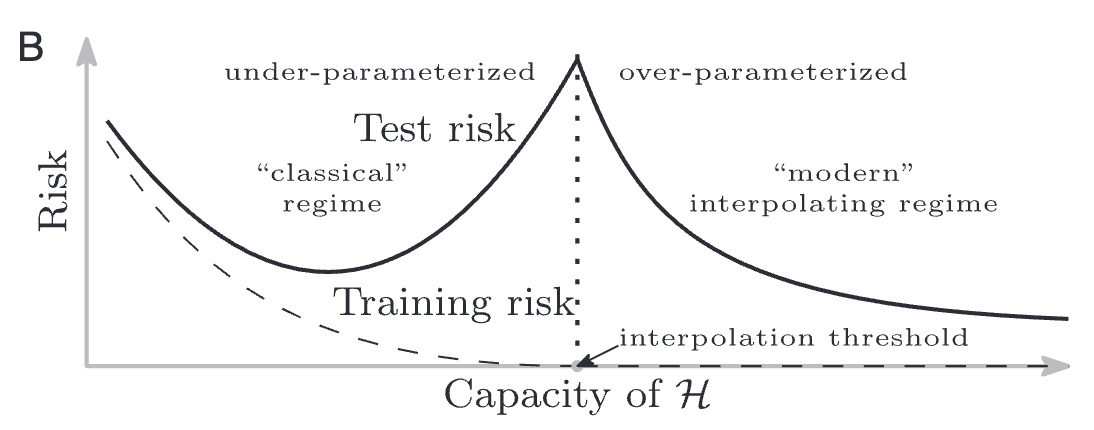
하지만 현대 딥러닝의 실제 현장에서는 이상한 현상이 점점 관측되고 있다. 수백만, 수억 개의 파라미터를 가진 거대한 모델들이 training data를 완벽하게 예측하면서도(training loss = 0), 놀랍게도 test data에서 준수한 성능을 보인다. 이 지점은 기존 optimal 지점보다도 이후 지점에 발생하고, 기존 optimal 지점보다 성능이 훨신 좋을 수도 있다. 이는 고전 이론으로는 설명할 수 없는 현상이기도 하다.

기존 개념에서 Bias-variance tradeoff를 설명할때 다음의 식을 관찰하며 그래프를 본다.

$$ \text{Risk} = \text{Bias}^2 + \text{Variance} + \sigma^2$$

Bias : 모델의 표현력 부족으로 인한 오차 (Parameter 수가 증가하면 감소)
Variance : 모델이 training data의 노이즈에 민감하게 반응하는 정도 (Parameter 수가 증가하면 증가)
$\sigma^2$ : 고정 오차 (Irreducible Error)

그런데 2019년 Belkin et al. 의 연구에서 Parameter 수가 매우 큰 경우 위와 같은 식의 경향이 바뀐다는 것을 발견했다.

Double Descent 현상을 나타내는 그래프. Belkin et al. 2019

왜 Double Descent가 일어나는가?

왜 이런 현상이 일어나는지 논문에서는 다음과 같이 이야기한다.

Training loss를 최소화하는 Weight 종류가 Parameter가 커지면 더 많아짐
거기에 대부분의 알고리즘은 그 중 Weight가 최적화되는 (e.g. 가장 작은 norm을 가진) 기존보다 더 좋은 weight를 선택함
추가로 Parameter가 많으면 weight를 통해 더 smooth한 function을 만들 수 있다.

언제 Double Descent가 일어나는가?

직접적으로 Parameter 수를 늘릴 때
이미 Over-Parameterized model에서 training sample 수를 늘릴 때
Over-Parameterized model + Fixed training sample 수에 training epoch를 늘렸을 때

이때 Over-Parameterized Model은 Loss function 값을 0으로 만드는 파라미터가 존재하는 모델을 기준으로 하고, 이 기준을 interpolation threshold라고 한다.

Double Descent를 어떻게 활용할 수 있을까?

이런 현상을 다음과 같이 해석할 수 있을것이다.

모델이 interpolation threshold를 넘어설 만큼 충분히 크다면, 더 크게 만드는 것이 성능을 해칠 가능성이 낮다고 볼 수 있다. 이는 GPT, BERT 같은 거대 모델들의 성공을 설명해주기도 한다.
Epoch 기반 Double Descent를 생각한다면, validation loss가 올라간다고 바로 멈추기보다는 더 기다려볼 필요성이 생긴다.

Bigger is better, sometimes

Double Descent는 현대 머신러닝이 왜 작동하는지에 대한 하나의 이유가 되었다. 전통적인 통계 이론이 예측하는 것과 달리, 실제 딥러닝 현장에서는 "bigger is better"가 성립하는 경우가 많다. 하지만 이것이 무조건 큰 모델을 만들라는 의미는 아니다. Interpolation threshold 근처는 여전히 위험한 영역이며, 모델 설계 시 이를 고려해야 한다. 이후 모델을 학습시킬 때 loss 그래프를 유심히 관찰해서 이런 현상이 발생하는지 확인해봐야 될 것 같다.

참고문헌

Belkin, Mikhail, Daniel Hsu, Siyuan Ma, and Soumik Mandal. 2019. “Reconciling Modern Machine-Learning Practice and the Classical Bias-Variance Trade-Off.” Proceedings of the National Academy of Sciences of the United States of America 116 (32): 15849–54.