ML에서 Cosine Similarity를 사용할 땐 주의가 필요하다

Cosine similarity는 벡터의 각도만 측정하여 크기를 무시하므로, 독립 확률변수 간에도 높은 유사도를 나타내는 등 예상과 다른 결과를 낳을 수 있다. 유사도 측도 사용 시 그것이 측정하는 "유사성"이 분석 목적과 일치하는지 반드시 확인해야 한다.

ML에서 Cosine Similarity를 사용할 땐 주의가 필요하다
Photo by Etienne Girardet / Unsplash

최근 국가에서 독자AI파운데이션 모델을 개발하기 위해 여러 회사에서 경쟁하며 모델들을 개발하고 있다. 그중 5개 정예팀으로 선정된 기업 중 유일한 중소기업인 Upstage에서 작년 연말 이에 대한 성과 모델인 Solar-Open-100B가 공개되었는데 이에 대해 타 LLM 모델(GLM-4.5-Air)과 파라미터의 유사도가 높다는 주장이 있어 Solar 모델이 파운데이션 모델이 맞는지에 대한 논란이 있었다. 주장의 핵심은 두 모델의 같은 레이어의 Layernorm 파라미터의 Cosine similarity값이 0.989로 매우 높게 나와 이는 Solar 모델이 from scratch 모델이 아니라는 통계적 이상치라는 것이였다.

위 주장에 대해 여러 의견이 나왔고, 실제 Upstage에서도 이를 검증하는 공개 검증세션을 열어 위 주장이 오류가 있다고 밝혀 위 논란은 어느정도 정리가 되었다. 이번 글에서는 좀더 심화 단계인 모델의 Parameter 비교에 대해서는 추후 다뤄보기로 하고, 이 주장의 오류 중 어느정도 영향력이 있었던 Cosine similarity에 대해 정리하고 이를 사용하는데 어떤 점을 주의해야 하는지에 대해서 정리해 보았다.

Cosine similarity란

Cosine similarity

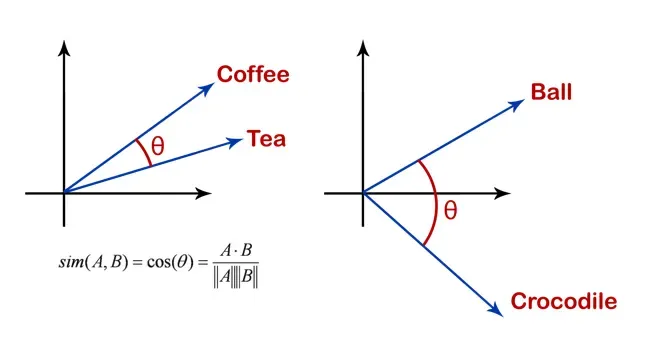
Cosine similarity는 두 벡터 사이의 유사도를 측정하는 측도(measure)이다. 이때 명칭 그대로 cosine 값을 사용하는데, 직관적으로 이해한다면 두 벡터 사이의 각을 표현한다고 볼 수 있다. (물론 실전에서 고차원 벡터 사이의 cosine similarity는 기하학적으로 해석하긴 어렵다.) 공식을 보자면 아래와 같이 표현할 수 있다.

$$ S_C(A, B) := \cos(\theta) = \frac{A\cdot B}{\lVert A \rVert \lVert B \rVert} $$

이 측도는 주로 LLM에서 vector로 embedding된 단어, 텍스트 간 유사도를 비교하는 지표로 사용되고 있다. 텍스트 그 자체로 비교(길이 등)한다면 의미가 유사한 텍스트를 구분할 수 없지만, embedding된 vector로 서로 비교할때 cosine similarity를 사용한다면 간단하고 빠르게 vector 비교를 할 수 있다.

Embedding vector 비교로 cosine similarity를 사용할 때의 문제​점

다만 cosine similarity로 비교하다가는 여러 문제를 발견할 수 있다. 이 글의 예시를 보자면 "What did I do with my keys?" 에 대한 비교 문장으로

  • "I left them in my pocket"
  • "They are on the table"
  • "What did I put my wallet?"
  • "What I did to my life?"

를 비교해 보았더니 가장 가까운 문장은 "What I did to my life?" 이였다. LLM와 같은 모델에서는 위 질문 문장에 대해 유사한 문장으로 답변 문장을 원하지만, embedding된 vector들의 cosine similarity로 비교한 문장들은 문장 구조에 꽤나 의존하는 결과가 나온 것이다.

이런 예시도 있다. word2vec은 결국 데이터를 학습해 embedding을 하도록 만들어놨으니, 학습한 데이터에 의존된 결과를 낼 수 밖에 없다. 그 상황에서 "espresso"와 "cappuccino"는 매우 유사하게 결과가 나오지만, 사용하는 문화에 따라서, 이탈리아에서는 두 단어를 엄밀하게 다르게 보기에 cosine similarity에 의존하기엔 힘들다.

위와 같은 문제들을 종합하자면, cosine similarity로 유사성을 수치화할 수 있지만, 이 수치가 우리가 원하는 유사성의 정의와는 매우 동떨어질 수 있다. 데이터마다, 모델마다 원하는 유사성이 있을것이고, 이에 대해 cosine similarity가 명확히 그 유사성을 표현할수 있는지는 위 예시와 같이 추가적인 실험이 필요한것이다.

Cosine similarity가 잡지 못하는 유사성

좀 더 기본적인, 간단하고 데이터 도메인에 의존하지 않은 간단한 예시를 임성빈 교수님의 링크드인 글에서 소개해주셨다. 평균이 0 이고 분산이 $\sigma^2$인 두 확률변수 X 랑 Y 가 서로 독립일 때, 1+X와 1+Y의 cosine similarity를 계산해보면

$$ S_C(1+X, 1+Y) := \frac{\mathbb{E}[(1+X)(1+Y)]}{\sqrt{\mathbb{E}[(1+X)^2]}\sqrt{\mathbb{E}[(1+Y)^2]}} = \frac{1}{1+\sigma^2}$$

이는 $\sigma^2 \to 0$일 때 cosine similarity가 1이 된다는 이야기이다. 그런데 반대로 통계에서 많이 사용하는 상관계수를 1+X와 1+Y에 대해서 본다면 X와 Y가 독립이므로 당연히 0이 나온다. cosine similarity가 만사 다 통하는 유사성 측도가 아니라는 것이다.

측도를 선택한다는 것의 의미

유사도 측도를 선택할 때는 해당 측도가 측정하는 "유사성"이 무엇인지, 그리고 그것이 우리가 분석하고자 하는 문제에서 의미 있는 유사성인지를 먼저 정의해야 한다. Cosine similarity를 사용한다면 벡터의 방향성만을 비교한다는 점을 명확히 인지하고, 필요에 따라 상관계수, Euclidean distance 등 다른 측도와 병행하여 다각도로 분석하는 것이 바람직하다.

이번 논란에 대해 반론으로 작성한 글 에서는 파라미터 비교를 상관계수, L1 & L2 distance, 절댓값 분포의 99 percentile차이, CV(Coefficient of Variation) 차이 등 다양한 측도를 활용해 반론했다. 이와 같이 모델 파라미터 비교와 같은 민감한 분석에서는 단일 측도에 의존하기보다는 데이터의 통계적 특성, 분포, 그리고 도메인 지식을 종합적으로 고려한 검증이 필수적이다.

참고자료